The happiest thought of my life.

In 1907, only two years after the publication of his Special Theory of Relativity, Einstein wrote a paper attempting to modify Newton's theory of gravitation to fit special relativity. Was this modification necessary? Most emphatically yes! The reason lies at the heart of the Special Theory of Relativity: Newton's expression for the gravitational force between two objects depends on the masses and on the distance separating the bodies, but makes no mention of time at all. In this view of the world if one mass is moved, the other perceives the change (as a decrease or increase of the gravitational force) instantaneously. If exactly true this would be a physical effect which travels faster than light (in fact, at infinite speed), and would be inconsistent with the Special Theory of Relativity (see Sect. 6.2.7). The only way out of this problem is by concluding that Newton's gravitational equations are not strictly correct. As in previous occasions this does not imply that they are ``wrong'', it only means that they are not accurate under certain circumstances: situations where large velocities (and, as we will see, large masses) are involved cannot be described accurately by these equations.

In 1920 Einstein commented that a thought came into his mind when writing the above-mentioned paper he called it ``the happiest thought of my life'':

The gravitational field has only a relative existence... Because for an observer freely falling from the roof of a house - at least in his immediate surroundings - there exists no gravitational field.

Let's imagine the unfortunate Wile E. Coyote falling from an immense height [*]. As he starts falling he lets go of the bomb he was about to drop on the Road Runner way below. The bomb does not gain on Wile nor does it lag behind. If he were to push the bomb away he would see it move with constant speed in a fixed direction. This realization is important because this is exactly what an astronaut experiences in outer space, far away from all bodies (we know, the Apollo's 10-13 spacecrafts did travel far from Earth).

Mr. Coyote is fated to repeat the experience with many other things: rocks, magnets, harpoons, anvils, etc. In all cases the same results are obtained: with respect to him all objects, irrespective of composition, mass, etc. behave as if in free space. So, if he should fall inside a closed box, he would not be able to tell whether he was plunging to his death (or, at least, severe discomfort), or whether he was in outer space on his way to Pluto at constant speed.

This is reminiscent of Galileo's argument: the observer lets go of some objects which remain in a state of uniform motion (with respect to him!). This behavior is independent of their chemical or physical nature (as above, air resistance is ignored). The observer (Wile), as long as he confines his/her observations to his/her immediate vicinity (that is, as long as he/she does not look down) has the right to interpret his state as `at rest'. Just as Galileo argued that experiments in a closed box cannot determine the state of uniform motion of the box, Einstein argued that experiments in a freely falling small[*] closed box cannot be used to determine whether the box is in the grip of a gravitational force or not.

Why would this be true? The answer can be traced back to the way in which gravity affects bodies. Remember (see Sect. 4.3.3) that the quantity we called m (the mass) played two different roles in Newton's equations. One is to determine, given a force, what the acceleration of the body would be: F = m a (the inertial mass). The other is to determine the intensity with which the said body experiences a gravitational force: F = m M G / r2 (the gravitational mass). As mentioned before these two quantities need not be equal: the first ``job'' of m is to tell a body how much to accelerate given any force, a kick, an electric force (should the body be charged), etc. The second ``job'' tells the body how much of the gravitational force should it experience and also determines how strong a gravitational force it generates. But, in fact, both numbers are equal (to a precision of ten parts per billion).

What does this imply? Well, from Newton's equations we get

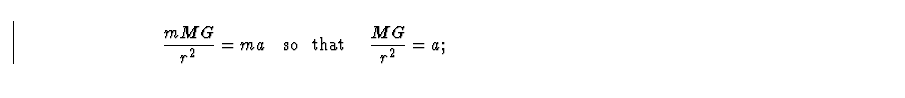
\begin{displaymath} { m M G \over r^2 } = m a \quad \hbox{so \ that } \quad { M G \over r^2 } = a ; \end{displaymath}

this equation determines how a body moves, which trajectory it follows, how long does it take to move from one position to another, etc. and is independent of m! Two bodies of different masses, composition, origin and guise will follow the same trajectory: beans, bats and boulders will move in the same way.

So the equality of the two m's was upgraded by Einstein to a postulate: the Principle of Equivalence; this one statement (that the m in m a and the m in m MG/r2 are identical) implies an incredible amount of new and surprising effects. The m in F=ma is called the inertial mass and the m in m M G/r2 the gravitational mass. Then the Principle of Equivalence states that

the inertial and gravitational masses are identical.

The whole of the General Theory of Relativity rests on this postulate, and will fail if one can find a material for which the inertial and gravitational masses have different values. One might think that this represents a defect of the theory, its Achilles heel. In one sense this is true since a single experiment has the potential of demolishing the whole of the theory (people have tried...hard, but all experiments have validated the principle of equivalence). On the other hand one can argue that a theory which is based on a minimum of postulates is a better theory (since there are less assumptions involved in its construction); from this point of view the General Theory of Relativity is a gem [*].

The completed formulation of the General Theory of Relativity was published in 1916 (Fig. 7.2).


 
Figure 7.2: Einstein's General Theory of Relativity paper.  
\begin{figure} \centerline{ \vbox to 2.5 truein{\epsfysize=2.5 truein\epsfbox[0 0 612 792]{7.gtr/gr_paper.ps}} }\end{figure}