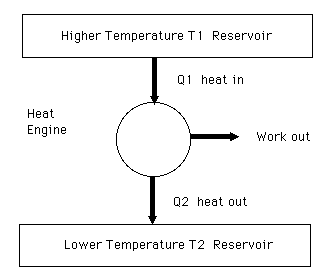
Schematic diagram of a standard heat engine.
Most engines used in modern society are heat engines. This includes steam electric power generators, automobiles, trucks, many locomotives, refrigerators, air conditioners, heat pumps.
The first recorded heat engine was that made by Hero of Alexander in AD 50.The first major step toward the mechanization of society was the invention of the steam engine by James Watt in 1765/1769. Over the years improvement and modifications were made to the steam engine and it became a major force in the industrial revolution. As the steam engine developed becoming more reliable and powerful interest turned towards making it more efficient. A major factor in cost is the fuel efficiency and it occupied a significant amount of the engineers efforts.
The efficiency of a heat engine is defined as the work out divided by the energy in.
Efficiency = (Work out) / (Energy in) = (Work out) / (Heat in)
by conservation of energy this is also
Efficiency = (Heat in - Heat out) / (Energy in) = 1 - (Heat out) / (Heat in)
In 1824 French engineer Sadi Carnot (1796-1832) wrote and published a monograph entitled "Reflexions sur la Puissance motrice du Feu" (Reflections on the Motive power of Fire). In his treatise Carnot brilliantly reasoned the general principles regarding the efficiency of heat engines. In the best traditions of the French Cartesian school (followers/admirers of Rene Descartes), Carnot started with a simple assumption and derived the implications applicable to essentially all engines.
Carnot's Assumption: Heat cannot be taken in at a certain temperature and converted to work with no other change in the system of surroundings.
(This is equivalent to the other formulations of the second law of thermodynamics listed previously.)
Definition of an engine: A engine works in a closed cycle, returning to its initial state periodically at the end of each cycle. It is an energy transformer acting as a catalyst. In a chemical reaction a catalyst works by combining with one of the initial constituent atoms or molecules and undergoing a series of reactions until the desired compound is formed and the catalyst is released in its initial form to begin its actions anew. dust.
Schematic diagram of a standard heat engine.
Carnot thought about what would be the absolute maximum efficiency for a heat engine. One needs to consider an idealized heat engine. We need to do what Galileo did when he thought about frictionless motion beginning the understanding of motion. The idealized heat engine is one that is operated in a reversible manner and has no internal friction and inefficiencies but those that are fundamental. By reversible we mean that there are no changes in the system (that includes the engine and the two heat baths and the work energy) that cannot be reversed with only an infinitesimal change. In frictionless motion a body in very slight motion in one direction can have its direction reversed by the application of a very small impulse. A ideal reversible heat engine can have its direction of operation reversed with only very minor changes.
Schematic diagram of a reversible heat engine operating in forward and reversed - refrigerator - mode. This is essentially how a home heat pump works.
This is proved by assuming that there is a super heat engine with greater efficiency and showing that it contradicts Carnot's assumption.
Consider the case where both the reversible heat engine and the super heat engine remove the same amount of heat energy from the hot reservoir. If the reversible heat engine delivers work out W and deposits heat Qc = Q - W in the colder reservoir, then the super heat engine delivers work Ws = W+DW - additional work for the same heat input because it is more efficient - and heat Q = Q - W - DW to the cold reservoir. Note that the super heat engine puts less heat into the cold reservoir because its greater efficiency turns more of the original heat into its extra work. Now if we operate the reversible heat engine in reverse taking W of the W+DW work from the super heat engine to operate taking Qc out of the cold reservoir and putting Q into the hot one. The combined operation of the two engines results in no change in the hot reservoir since one takes out Q and the other puts back Q. Heat energy is taken out of the cold reservoir since the reversible heat engine takes out slightly more than the super heat engine puts in and it shows up as extra work. This taking heat from a single reservoir and turning it to work with no other changes is a contradiction to the Carnot assumption. Thus to stay consistent:
This is proved by showing that there is a contradiction, if they do not. We set the two heat engines to be compared operating between the same two heat reservoirs. Assume one is more efficient than the other. Run the less efficient one in reverse (as a refrigerator) using the fraction of the work from the more efficient engine that the less efficient engine would produce running forward. At that point there is zero net heat flow from the hot reservoir and the differential in work between the two engines is comes from the net heat removed from the cold heat reservoir. This contradicts the Carnot assumption. Thus to stay consistent:
Thus the revesible two heat engine system working between three reservoirs will have the same efficiency as the single reversible heat engine operating between the hottest and the coldest reservoirs.
If the first and second engine take the same heat Q1 from the hotest reservoir, then the reversible two heat engine system will convert the same fraction of the heat to work W13 = W12 + W23 and will reject the same heat Q3 to the lowest temperature (T1) heat reservoir.
We can now use this and conservation of energy to determine how much heat is deposited and removed from the middle temperature heat reservoir. We then will be able to obtain the relationship betwen fthe efficiencies of the heat engines running between the various temperatures.
Consider what happens when we run the third of the reversible heat engines backward. The first reversible heat engine running forward plus the third reversible heat engine running backwards must be equivalent to the second running forward.
The work W13 from the first heat engine minus the work needed to run the third heat engine backwards must equal the work out of the second heat engine. Combining this with conservation of energy:
Now we have the relationship to relate the heat absorbed at T1 to the heat delivered at T2 by finding the heat delivered to a third temperature T3. In the example we just considered, If one reversible heat engine absorbs heat Q1 at temperature T1 and delivers the heat Q3 at temperature T3, then a reversible heat engine that absorbs heat Q2 at temperature T2 will deliver the same heat Q3 to temperature T3.
We find these relationships for a full series of temperatures -
heat Qi absorbed at temperature Ti will deliver the same heat Q3 at temperature T3.
We only ned to define one temperature as the standard temperature
and we can relate the heat extracted by a reversible heat engine at any other temperature.
If a reversible heat engine absorbs the amount of heat Q at temperature T then it delivers an amount Qs at our standard temperature Ts. The amount it delivers is set by its Carnot efficiency.
We now have what is necessary to define a temperature scale.
If a reservoir is hotter then heat extracted by a reversible engine will be greater for a fix amount of heat delivered to our standard temperature. Thus F(T) and the efficiency are increasing functions of the reservoir temperature.
Lord Kelvin (William Thomson 1824-1907) suggested using this relationship to define a new temperature scale based upon this thermodynamic definition that F(T) = T / Ts so that
The remarkable thing is that the thermodynamic scale matches precisely with the temperature scale set by the ideal gas law.
One can conceive of a reversible heat engine whose working elements are an ideal gas and a frictionless piston volume.
The Carnot cycle is worked out in detail for an ideal gas and leads
directly to the same relationship
A Reversible Heat Engines has the maximum efficiency
No heat engine can have efficiency greater than a reversible heat engine.
All Reversible Heat Engines have same efficiency when operating between the same two temperature reservoirs.
Every reversible heat engine operating between the same two temperature reservoirs have identical efficiency.
This means no matter how a reversible heat engine is constructed or what the working fluid is, its efficiency is the same as all other heat engines working from the same two temperatures.
The Efficiency of a Reversible Heat Engine and the Thermodynamic Temperature Scale
Now we can go through a set of arguments that shows that one can
derive a relationship between the efficiency of reversible heat engines operating between three different temperature reservoirs.
Consider the case where we connect three heat engines so that one goes directly from the hottest temperature T1 reservoir to the coldest temperature T3 reservoir. The second heat engine is connected between the hottest (T1) to the middle (T2) temperature heat reservoir. The third heat engine is connected between the middle (T2) temperature reservoir and the coldest temperature (T3) reservoir. The efficiency of the two working in tandem must be equal to the efficiency of the first engine. Otherwise one could arrange things so that which ever chain has the highest efficiency (most work out for given heat in from the hottest (T1) temperature reservoir is run forward to produce work and a portion of that work used to run the other backward to put the heat into the hottest reservoir.
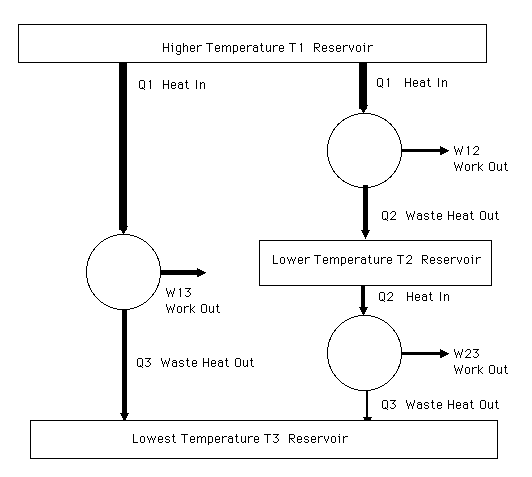Schematic diagram of reversible heat engines operating between three different temperature heat reservoirs.
W13 - W32 = (Q1 - Q3) - (Q2 - Q3) = Q1 - Q2 = W12
Efficiency = 1 - (Heat Out) / (Heat In) = 1 - Qs / Q
or
Qs = (1 - Efficiency) Q
or since we are referring our efficiency to a standard temperature Ts the efficiency can only depend upon the temperature T. And for a fixed heat input into the reservoir at our standard temperature Ts
the heat that is extracted at temperature T depends only upon that temperature:
Q = Qs /(1-Efficiency) = Qs F(T)
Q = Qs T / Ts or Q/T = Qs/Ts
The division by Ts makes it so that the heat drawn out from Ts matches the heat put back into Ts since the Carnot assumption is that we cannot take heat out of a single temperature bath and obtain work without any other changes.
We find that for all reversible heat engines we have the relationship
that the efficiency is equal to one minus the ratio of the cold reservoir thermodynamic temperature (Tc) and the hot reservoir thermodynamic temperature (Th)
Efficiency = 1 - Tc/Th
and
Q1/T1 = Q2/T2 = Q3/T3 = constant = S.
Q = S T
This constant S is given the name entropy. The entropy is constant for a reversible process but is not for one that is not. The entropy tends to increase in irreversible processes.
Efficiency = 1 - (Heat Out) / (Heat In) = 1 - Tc / Th
where the temperatures Tc and Th are the temperatures that are used in the ideal gas law:
PV = N k T