Experiment 5: A light clock lies on its side on a railroad car as the car moves to the left with velocity v.




Question: How is the length of the clock affected?

Answer: We know that the time between ticks on the moving clock, as we see it, will be t´ = . Let,

t1 = time that takes the light to go from the first mirror to the second , as we perceive it.
t2 = time that it takes the light to go from the second mirror back to the first, as we perceive it.
L´= length of the light clock, as we perceive it.

We can analyze the situation as follows:




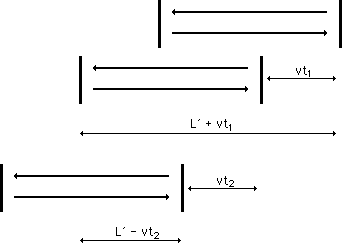
From the above picture we see that the distance the light traveled in time t1 was L´+ vt1. However, this distance is also equal to ct1 (rate x time). Also, the distance the light traveled on the return trip was L´- vt2 = ct2. Solving for t1, we have

L´+ vt1 = ct1

which implies that L´= ct1 - vt1,

which implies L´= (c - v)t1,

which implies t1 = .

Similarly,

L´- vt2 = ct2

which implies that L´= ct2 + vt2,

which implies L´= (c + v)t2,

which implies t2 = .

Thus,

t´ = t1 + t2


=


=


=


which implies that = .

Since t = (2L)/c,

=


which implies that = ,


which implies = ,


which implies = ,


which implies L´ = L .


Conclusion: Since is less than 1, this shows that we will measure the length of his light clock as being less than ours. Thus, when an object is moving in a straight line with a fixed velocity v, we will see its length, as measured in the direction in which it is moving, shorten.