Problem Set 1

Prof. Smoot's Physics 139 class

Due Week January 25, 1999

1. (1.2 Mould) Light from a distant star approaches the earth at an angle theta. The light enters the open end of a terrestrial telescope that is inclined at an angle theta-prime.

(a) Show that:

tan(theta-prime) = sin(theta) /[b + cos(theta)]

where b = v/c, and v is the velocity of the earth relative to the fixed stars. Find also the relativisitic formula taking into account length contraction.

(b) Find the expresion for tan(theta-prime), when v/c << cos(theta)

(c) Suppose b = v/c = 0.5. How would the appearance of the canopy of stars be distorted? Check for theta = w = 0, 45, 90, 135, and 180 degrees finding theta-prime in each case. What value of theta gives theta-prime = 90^o.

2. (1.4 Mould) Let the leg of the Michelson-Morley apparatus along the x -axis be equal to L₁, and the leg along the y axis be equal to L₂. The earth's velocity relative to the ether is v. Show that the fringe shift for a 90^o rotation is: n = b² (L₁ + L₂) / lambda where b = v /c. A 90^o rotation is the difference in difference in phase shifts for the interferometer aligned with motion and rotated 90^o.

3. (1.5 Mould) Michelson and Morley did not actually use a length L = 11 m in their apparatus. Both lengths ( L₁ and L₂) were folded back on themselves a number of times with mirrors. Show that if the length L₁ is folded in two, with both parts along the x -axis, the time for light to go back and forth over the complete path is still equal to: t = 2 L₁ / [c (1 - b²)] ~ 2 L₁ (1 + b²)/c.

4. (1.6 Mould) Show that FitzGerald's contraction hypothesis explains the result of the Michelson-Morley experiment (limit your proof to the case L₁ = L₂). What happens if L₁ is not equal to L₂? Does FitzGerald's contraction still explain the experimental result?

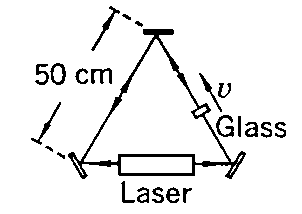
5. ( 2-3 French) In a modern Fizeau experiment (see French for a description of the original experiment), a laser is in one arm of a triangular arrangement of mirrors (see figure). A slab of glass (n =1.5) 1 cm thick is inserted in another arm of the system. The laser light can travel in a closed path in either direction. When the slab is moved with a speed of 1 cm/sec in the direction indicated. What is now the optical path difference? (This difference which can be converted to an audible beat note if the samples of the counter-circulating beams are suitably combined in a detector.) Note: this differs importantly from the original Fizeau arrangement in that the boundaries of the medium change position while the light passes through. Your calculation must take account of this fact.