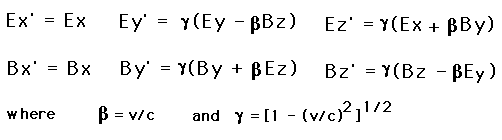
1. The Doppler Shift: Calculate the frequency one would observe for for two neutron star pulsars, pulsing at 1000 Hz, mass 1.4 solar masses, and orbiting each other at 20 Hz.
2. Charged Particle Dynamics:
(a) Solve the equations of motion of a charged particle moving non-relativistically in the x-y plane in the presence of a uniform electrostatic field E in the y direction and a uniform magnetostatic field B in the z direction. Assume E < B and and use units such that the Lorentz force is F = q(E + v x B). The particle starts at rest at t = 0 at the origin.
(b) Repeat the calculation in a coordinate system moving uniformly with respect to the first with velocity V = c (E x B)/B^2.
(c) Repeat (a) using the dynamics of special relativity. State the conditions under which solution (c) must be used instead of solution (a).
(d) Examine the case E > B carefully, finding where modifications must be made in each of the preceding cases. Obtain a complete and accurate solution in this case by the simplest method you can find.
3. Electromagnetic Field Transformations: The transformation equations for electric and magnetic fields are that the parallel electric and magnetic fields are unchanged but the perpendicular fields are boosted by gamma and modified by the transform velocity times the other. e.g.
E'|| = E|| B'|| = B||
E'perp =
In this specific case this becomes:
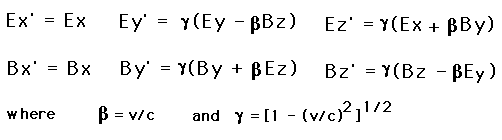
The field of a point charge in its rest frame S' is the Coloumb field:
E' = q r /|r|^3
B' = 0
From these find the electric and magnetic fields of the charge at r in the laboratory frame S in which it is moving with constant velocity V. [The fields should be inversely proportional to s^3, where s^2 = |r - Vt|^2 + (gamma^2 -1) (x - Vt)^2.
4. Find the electromagnetic field tensor, F^{mu nu}, and the stress-energy tensor T_{\mu \nu} for a particle at rest with mass, m_o, and charge, q. (See problem 3 for hint and help.)
What would these be for an observer moving with a velocity, v, in the x-direction?
5. Use the result of Problem 3 or 4 to calculate the force on an initially stationary electron (q = -e) when a fast charged particle (q = +/- Ze) flies by with speed v at an "impact parameter" b. In this calculation, neglect the displacement and velocity of the electron as well as the change in velocity of the fast particle during the collision. By integrating the force with respect to time, show that the electron acquires transverse momentum of magnitude
2Ze^2/bv
Show that a nonrelativistic treatment (c-> infinity) gives the same result for the impulse to the electron, although the effective duration of the collision and the peak transverse force are different. Show that the energy loss of the fast particle (equal to the kinetic energy gained by the electron) is proportional to (Z/bv)^2 and is independent of its proper mass.