This page indicates how the Greeks made the first real measurements of astronomical distances---the size of the earth and the distance to the moon, both found rather well, and the distance to the sun, where the first estimate was far off but their eventual best estimate fell short by a only factor of two.
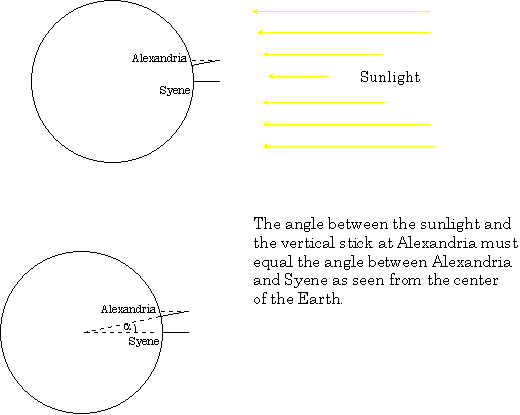
The first reasonably good measurement of the earth's size was done by Eratosthenes, a Greek who lived in Alexandria, Egypt, in the second century B.C. He knew that far to the south, in the town of Syene (present-day Aswan, where there is now a huge dam on the Nile) there was a deep well and at midday on June 21, the sunlight reflected off the water far down in this well, something that happened on no other day of the year. The point was that the sun was exactly vertically overhead at that time, and at no other time in the year. Eratosthenes also knew that the sun was never vertically overhead in Alexandria, the closest it got was on June 21, when it was off by an angle he found to be about 7.2 degrees, by measuring the shadow of a vertical stick.
The distance from Alexandria to Syene was measured at 5,000 stades (a stade being 500 feet), almost exactly due south. From this, and the difference in the angle of sunlight at midday on June 21, Eratosthenes was able to figure out how far it would be to go completely around the earth.

According to the Greek historian Cleomedes, Eratosthenes measured the angle between the sunlight and the stick at midday in midsummer in Alexandria to be 7.2 degrees, or one-fiftieth of a complete circle. It is evident on drawing a picture of this that this is the same angle as that between Alexandria and Syene as seen from the center of the earth, so the distance between them, the 5,000 stades, must be one-fiftieth of the distance around the earth, which is therefore equal to 250,000 stades, about 23,300 miles. The correct answer is about 25,000 miles, and in fact Eratosthenes may have been closer than we have stated here---we're not quite sure how long a stade was, and some scholars claim it was about 520 feet, which would put him even closer.
How do we begin to measure the distance from the earth to the moon? One obvious thought is to measure the angle to the moon from two cities far apart at the same time, and construct a similar triangle, like Thales measuring the distance of the ship at sea. Unfortunately, the angle difference from two points a few hundred miles apart was too small to be measurable by the techniques in use at the time, so that method wouldn't work.
Nevertheless, Greek astronomers, beginning with Aristarchus of Samos (310-230 B.C., approximately) came up with a clever method of finding the moon's distance, by careful observation of a lunar eclipse, which happens when the earth shields the moon from the sun's light.
To better visualize a lunar eclipse, just imagine holding up a quarter (diameter one inch approximately) at the distance where it just blocks out the sun's rays from one eye. Of course you shouldn't try this---you'll damage your eye! You can try it with the full moon, which happens to be the same apparent size in the sky as the sun. It turns out that the right distance is about nine feet away, or 108 inches. If the quarter is further away than that, it is not big enough to block out all the sunlight. If it is closer than 108 inches, it will totally block the sunlight from some small circular area, which gradually increases in size moving towards the quarter. Thus the part of space where the sunlight is totally blocked is conical, like a long slowly tapering icecream cone, with the point 108 inches behind the quarter. Of course, this is surrounded by a fuzzier area, called the "penumbra", where the sunlight is partially blocked. The fully shaded area is called the "umbra". (This is Latin for shadow. Umbrella means little shadow in Italian.) If you tape a quarter to the end of a thin stick, and hold it in the sun appropriately, you can see these different shadow areas.
Question: If you used a dime instead of a quarter, how far from your eye would you have to hold it to just block the full moonlight from that eye? How do the different distances relate to the relative sizes of the dime and the quarter? Draw a diagram showing the two conical shadows.
Now imagine you're out in space, some distance from the earth, looking at the earth's shadow. (Of course, you could only really see it if you shot out a cloud of tiny particles and watched which of them glistened in the sunlight, and which were in the dark.) Clearly, the earth's shadow must be conical, just like that from the quarter. And it must also be similar to the quarter's in the technical sense--- it must be 108 earth diameters long! That is because the point of the cone is the furthest point at which the earth can block all the sunlight, and the ratio of that distance to the diameter is determined by the angular size of the sun being blocked. This means the cone is 108 earth diameters long, the far point 864,000 miles from earth.

Now, during a total lunar eclipse the moon moves into this cone of darkness. Even when the moon is completely inside the shadow, it can still be dimly seen, because of light scattered by the earth's atmosphere. By observing the moon carefully during the eclipse, and seeing how the earth's shadow fell on it, the Greeks found that the diameter of the earth's conical shadow at the distance of the moon was about two-and-a-half times the moon's own diameter.
Note: It is possible to check this estimate either from a photograph of the moon entering the earth's shadow, or, better, by actual observation of a lunar eclipse.
Question: At this point the Greeks knew the size of the earth (approximately a sphere 8,000 miles in diameter) and therefore the size of the earth's conical shadow (length 108 times 8,000 miles). They knew that when the moon passed through the shadow, the shadow diameter at that distance was two and a half times the moon's diameter. Was that enough information to figure out how far away the moon was?
Well, it did tell them the moon was no further away than 108x8,000 = 864,000 miles, otherwise the moon wouldn't pass through the earth's shadow at all! But from what we've said so far, it could be a tiny moon almost 864,000 miles away, passing through that last bit of shadow near the point. However, such a tiny moon could never cause a solar eclipse. In fact, as the Greeks well knew, the moon is the same apparent size in the sky as the sun. This is the crucial extra fact they used to nail down the moon's distance from earth.
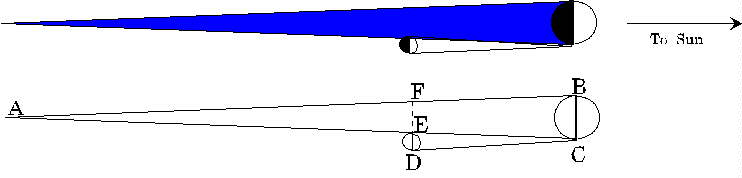
They solved the problem using geometry, constructing the figure below. In this figure, the fact that the moon and the sun have the same apparent size in the sky means that the angle ECD is the same as the angle EAF. Notice now that the length FE is the diameter of the earth's shadow at the distance of the moon, and the length ED is the diameter of the moon. The Greeks found by observation of the lunar eclipse that the ratio of FE to ED was 2.5 to 1, so looking at the similar isosceles triangles FAE and DCE, we deduce that AE is 2.5 times as long as EC, from which AC is 3.5 times as long as EC. But they knew that AC must be 108 earth diameters in length, and taking the earth's diameter to be 8,000 miles, the furthest point of the conical shadow, A, is 864,000 miles from earth. From the above argument, this is 3.5 times further away than the moon is, so the distance to the moon is 864,000/3.5 miles, about 240,000 miles. This is within a few percent of the right figure. The biggest source of error is likely the estimate of the ratio of the moon's size to that of the earth's shadow as it passes through.
This was an even more difficult question the Greek astronomers asked themselves, and they didn't do so well. They did come up with a very ingenious method to measure the sun's distance, but it proved too demanding in that they could not measure the important angle accurately enough. Still, they did learn from this approach that the sun was much further away than the moon, and consequently, since it has the same apparent size, it must be much bigger than either the moon or the earth.
Their idea for measuring the sun's distance was very simple in principle. They knew, of course, that the moon shone by reflecting the sun's light. Therefore, they reasoned, when the moon appears to be exactly half full, the line from the moon to the sun must be exactly perpendicular to the line from the moon to the observer (see the figure to convince yourself of this). So, if an observer on earth, on observing a half moon in daylight, measures carefully the angle between the direction of the moon and the direction of the sun, the angle a in the figure, he should be able to construct a long thin triangle, with its baseline the earth-moon line, having an angle of 90 degrees at one end and a at the other, and so find the ratio of the sun's distance to the moon's distance.
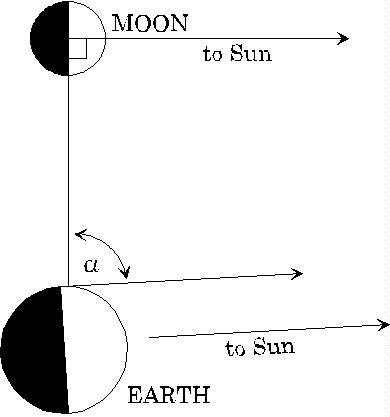
The problem with this approach is that the angle a turns out to differ from 90 degrees by about a sixth of a degree, too small to measure accurately. The first attempt was by Aristarchus, who estimated the angle to be 3 degrees. This would put the sun only five million miles away. However, it would already suggest the sun to be much larger than the earth. It was probably this realization that led Aristarchus to suggest that the sun, rather than the earth, was at the center of the universe. The best later Greek attempts found the sun's distance to be about half the correct value (92 million miles).
The presentation here is similar to that in Eric Rogers, Physics for the Inquiring Mind, Princeton, 1960.
NOTE TO TEACHERS: To see present-day schoolchildren reproducing Eratosthenes' results,