In the case of PSR 1913+16, the orbit is inclined at about 45 degrees with respect to the plane of the sky, and it is oriented such that periastron occurs nearly perpendicular to our line of sight.
(Figure from Weisberg et al. 1981)
Using the Arecibo 305m antenna, Hulse and Taylor detected pulsed radio emission and thus identified the source as a pulsar, a rapidly rotating, highly magnetized neutron star. The neutron star rotates on its axis 17 times per second; thus the pulse period is 59 milliseconds.
After timing the radio pulses for some time, Hulse and Taylor noticed
that there was a systematic variation in the arrival time of the
pulses. Sometimes, the pulses were received a little sooner than expected;
sometimes, later than expected. These variations changed in a smooth and
repetitive manner, with a period of 7.75 hours. They realized that such
behavior is predicted if the pulsar were in a binary
orbit with another star.
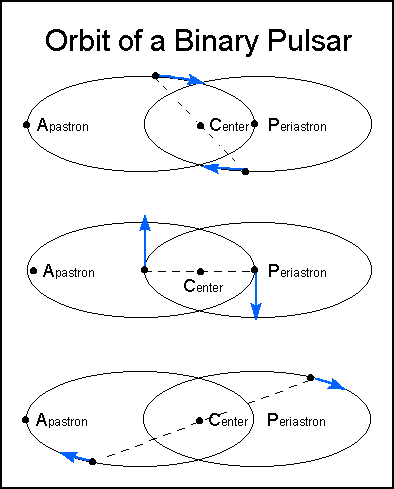
| The pulsar and its companion both follow elliptical orbits
around their common center of mass. Each star moves in its orbit according
to Kepler's Laws; at all times the two
stars are found on opposite sides of a line passing through the center
of mass. The period of the orbital motion is 7.75 hours, and the stars
are believed to be nearly equal in mass, about 1.4 solar masses. As shown
in the figure here, the orbits are quite eccentric. The minimum separation
at periastron is about 1.1 solar radii; the maximum separation at
apastron is 4.8 solar radii.
In the case of PSR 1913+16, the orbit is inclined at about 45 degrees with respect to the plane of the sky, and it is oriented such that periastron occurs nearly perpendicular to our line of sight. (Figure from Weisberg et al. 1981) |
 |
Remember that a star in an elliptical orbit will move slower when it
is at apastron than when it is a periastron. In an eccentric orbit such
as that of PSR 1913+16, the radial velocity varies from a minimum of 75
km/sec to a maximum of 300 km/sec. Hulse and Taylor used their timing measurements
of the pulses to infer the details of the orbital motion.
| The pulse repetition frequency, that is, the number of
pulses received each second, can be used to infer the radial velocity of
the pulsar as it moves through its orbit. When the pulsar is moving towards
us and is close to its periastron, the pulses should come closer together;
therefore, more will be received per second and the pulse repetition rate
will be highest. When it is moving away from us near its apastron, the
pulses should be more spread out and fewer should be detected per second.
(Figure from Weisberg et al. 1981) |
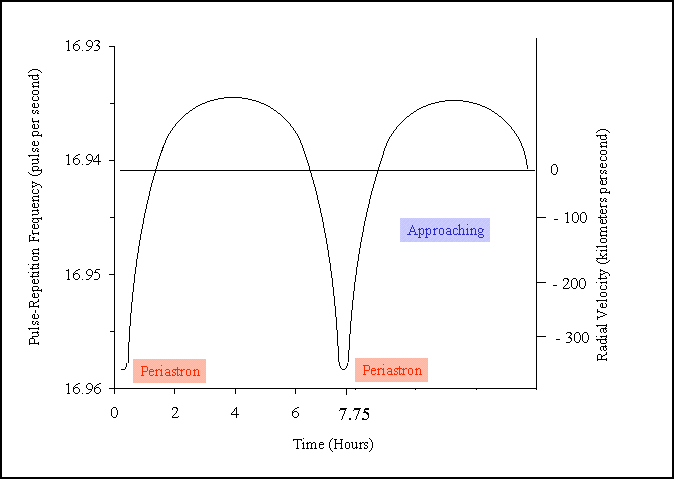 |
The fact that the negative velocities (blueshifts, approaching the Earth)
are larger than the postitive one (redshifts, moving away from Earth) show
that the orbit is highly eccentric.
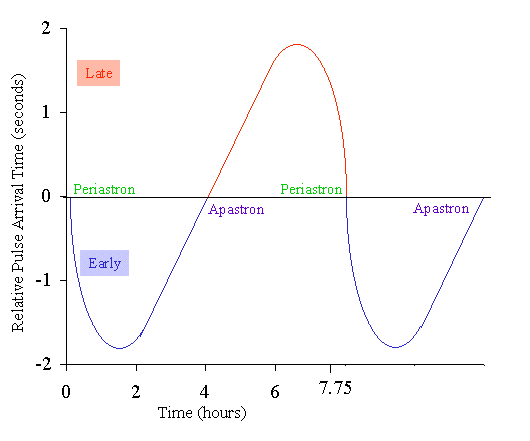
| The pulsar arrival times also vary as the pulsar moves
through its orbit. When the pulsar is on the side of its orbit closest
to the Earth, the pulses arrive more than 3 seconds earlier that they do
when it is on the side furthest from the Earth. The difference is caused
by the shorter distance from Earth to the pulsar when it is on the the
close side of its orbit. The difference of 3 light seconds implies that
the orbit is about 1 million kilometers across.
(Figure from Weisberg et al. 1981) |
 |
Since the pulsing of the radio emission from the pulsar can be likened
to ticks on a clock, Hulse and Taylor realized that they could look for
changes in the ticking caused by relativistic changes in the measurement
of time. As seen above, the pulsar's orbital speed changes by a factor
of four during its orbit. Likewise, since the orbit of the pulsar around
its companion is elliptical, the two are closer together at some times
than at others, so that the gravitational field alternately strengthens
at periastron and weakens at apastron. Thus the binary pulsar PSR1913+16
provides a powerful test of the predictions of the behavior of time perceived
by a distant observer according to Einstein's Theory
of Relativity.
| When they are closer together, near apastron, the gravitational
field is stronger, so that the pasage of time is slowed down -- the time
between pulses (ticks) lengthens just as Einstein predicted. The pulsar
clock is slowed down when it is travelling fastest and in the strongest
part of the gravitational field; it regains time when it is travelling
more slowly and in the weakest part of the field.
(Figure from Weisberg et al. 1981) |
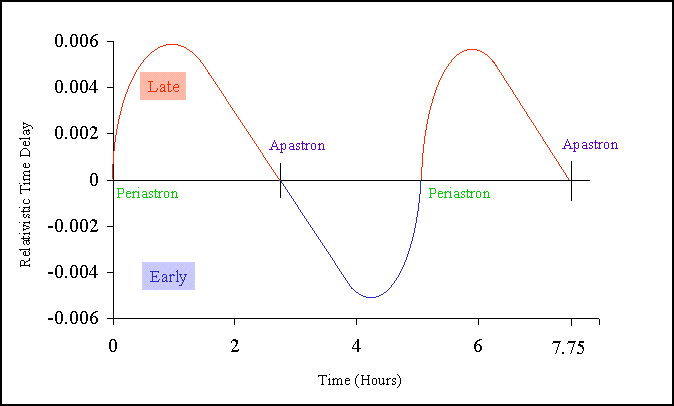 |
The relativistic time delay is the difference between what is observed and what one would expect to see if the pulsar were moving in circular orbit, at constant distance and at a constant speed, around its companion.
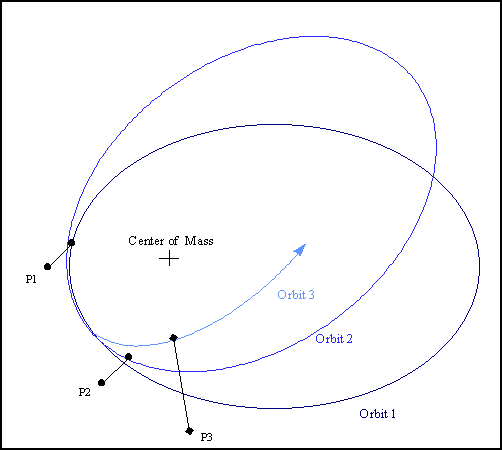
Space-time in the vicinity of the pulsar is greatly warped. This curvature causes the pulsar orbit to advance.
| The orbit of the pulsar appears to rotate with time; in
the diagram, notice that the orbit is not a closed ellipse, but a continuous
elliptical arc whose point of closest approach (periastron) rotates with
each orbit. The rotation of the pulsar's periastron is analogous to the
advance of the perihelion of Mercury in its
orbit. The observed advance for PSR 1913+16 is about 4.2 degrees per year;
the pulsar's periastron advances in a single day by the same amount as
Mercury's perihelion advances in a century.
(Figure from Weisberg et al. 1981) |
 |
Relativity predicts that the binary system will lose energy with time as orbital energy is converted to gravitational radiation.
| In 1983, Taylor and collaborators reported that there was
a systematic shift in the observed time of periastron relative to that
expected if the orbital separation remained constant. In the diagram shown
here, data taken in the first decade after the discovery showed a decrease
in the orbital period as reported by Taylor and his colleagues of about
76 millionths of a second per year. By 1982, the pulsar was arriving at
its periastron more than a second earlier than would have been expected
if the orbit had remained constant since 1974.
(Figure from Weisberg et al. 1981) |
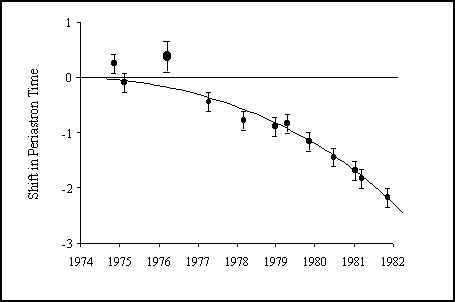 |
In the intervening decade, continued timing of the pulsar shows the continued decrease just as predicted by Einstein.
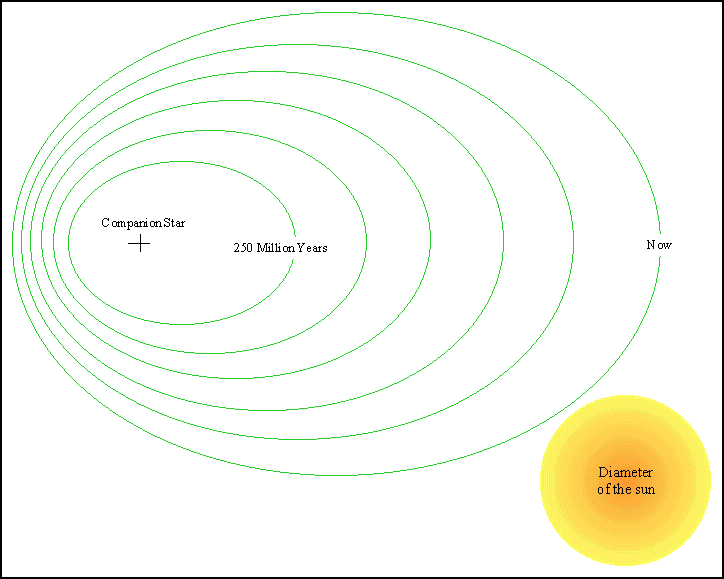
Because the binary system is losing energy, the orbits are shrinking,
and someday the two stars should coalesce. Such a merger might produce
strong enough gravitational radiation to be detected by instruments like
the Laser Inteferometer Gravitational-Wave
Observatory now under contruction.
| The pulsar's orbit is shrinking with time as shown in this
diagram; currently, the orbit shrinks by about 3.1 mm per orbit. The two
stars should merge in about 300 million years from now.
(Figure from Weisberg et al. 1981) |
 |
Further reading:
"The Binary Pulsar: Gravity Waves Exist", Will, C. 1987, Mercury, Nov-Dec, p. 162.
"Gravitational Waves from an Orbiting Pulsar", Weisberg, J.M., Taylor, J.H. and Fowler, L.A., 1981, Scientific American Oct, 74.