Physics 10 Lecture 3 Describing Motion

Professor Smoot's Class

Long Held Earth-centric Model

Early physics was mostly concerned with describing motion. The ancient Greeks had a well developed concept of motion. This was codified in Aristotle's books "Physics" and "Caelo" (Astronomy - literally sky or heavens). A brief summary of Aristotle's Physics (click on previous two words) is found at this connection and in the text book. It is a physics based upon observation, aethestics and common experience.

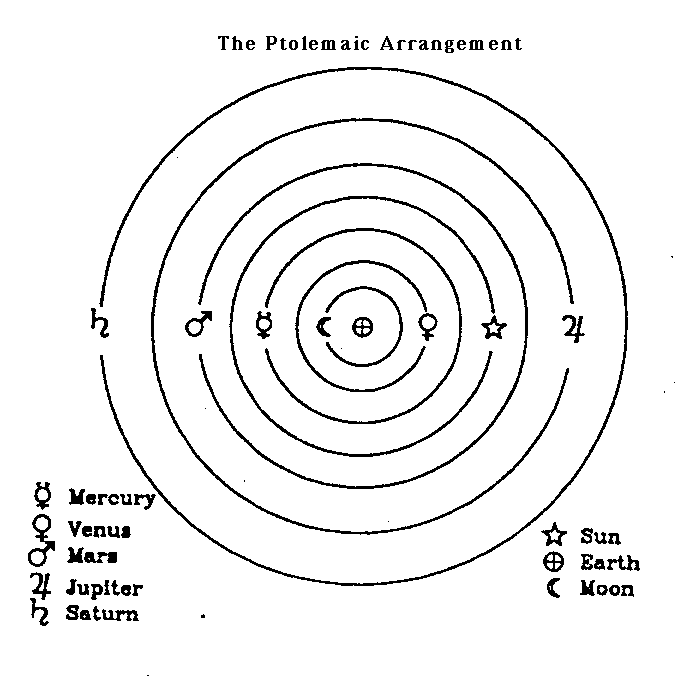
An important part of describing motion was describing the behavior of the heavens. The Greeks realized that the motion of nearly everything observed in the sky could be described very simply. All the stars were fixed relative to each other and seemed to rotate about the Earth each day (24 hour period). The dark night sky reminded them of the inside of a black bowl with bright lights attached. Thus the idea that all the stars were fixed upon a sphere which rotated about the Earth once per day.

Then there were other special cases, the Sun, the Moon, and the planets (a Greek word meaning wanderer). Clearly these too could be explained by simple uniform circular motion. Though the Greeks worked out a number of ways to describe the motion of the heavens, including one in which the Sun was at the center which was a Copernican view, the model that was accepted was the one which came to be call the Ptolemaic model. It was chosen on the basis of the accepted physics and observations - particularly the apparent lack of stellar parallax. This model held sway longer than any other scientific model in history even with the constant attention and observations of astronomers through out the millenia.

For all those centuries, until Johannes Kepler, astronomers, mathematicians, and scientists tried to describe the motions of the planets based upon three assumptions about planetary motion

The motion of all planets can be described by a series of circles.
The planets all travel with constant velocity about some point in space.
The orbits of the planets are all in the same plane,

None of these assumptions is correct.
The first two imply (or are based upon) that the planets move with uniform circular motions.

New View Develops
In the 1500's these concepts (assumptions) came under scrutiny and attack.

Nicholas Copernicus (1473-1543)
(photo) Nicholas Copernicus was a Polish-German clergyman. Most famous for developing a Sun-centered. Did need epicycles and reasons not accepted universally.

His work was presented as an aid to calculation, a "hypothesis." It was suggest that the calculation might be easier, if they were done "as if" the Earth revolved about the Sun. But the reader did not have to take this idea seriously. His book could probably not have been published without such a caution.
Europe at the time had become embroiled in the great turmoil of the Reformation and Counter-Reformation. A man's position on scientific matters could become a litmus test against which is loyalty was to be judged.
Copernicus had some rather poor data on which to base his tables. Calculation based on them did not make a very good fit the observed positions of the planets.
Copernicus felt it necessary to bring back a few of the epicycles that had made the Ptolemaic system so cumbersome. That was because he subscribed to the old ideas that motion of the heavens was circular and uniform.

Tycho Brahe (1546-1601)

Tycho Brahe was one of the greatest astronomical observers of all time. Clearly the most outstanding before the use of telescopes.
Tycho observed 11 November 1572 a supernova in the constellation Cassiopeia. The cosmology of the day was that the heavens, since they were created by God, were perfect and unchanging. It was inconceivable to an Aristotelian that a new star could appear in the immutable heavens (8th shell).
There had been a previous very bright supernova in 1006 AD so bright as to rival the moon followed a fifty years later, 1056 AD by the Crab supernova. These supernova were recorded by astronomers all over Asia and reputedly in the Americas. However, no European astronomer reported it. The only remarks seem to be about a bright comet which since the time of Aristotle had like meteors (hence the name from meteorology) thought to have been atmospheric phenomena.
The astronomers of Tycho's day refused to admit that it was a star (supernova) and in frustration Tycho is reputed to have said,
"O crassa ingenia, O coecos coeli spectatores." - translates "O thick wits, Oh blind watchers of the sky."

Tycho Brahe also observed the comet of 1577. Most astronomers used the method of Regiomontanus (1436-1476) to determine the parallax and thus the location
of the comment. Regiomontanus' method assumed
        (1) No intrinsic motion
        (2) no uncertainty in the timing of observations
        (3) the object could be observed on the meridian
Tycho Brahe not only made better observations but he developed a better method for determining the position of the comet from the observations. Tycho was able to show that the comet must pass through (and cracked) the crystalline spheres. This is a key point in the progress towards a more accurate description of the planets motion which was primarily a result of Tycho Brahe's own high quality observations.

Johannes Kepler (1571-1630)

Johannes Kepler, using the data from Taco Brahe, having set to the task of working on describing the orbit of Mars, came to realize the older assumptions were wrong and developed three new laws of planetary motion.

1st Law: Planets travel in elliptical orbits, with the Sun in the plane of the ellipse at one of the foci of the ellipse.
2nd Law: The planets move with a speed such that a line from the Sun to the planet sweeps out equal area in equal time.
3rd Law: The period of revolution of a planet increases as the distance from the Sun, in the mathematical proportion of the period squared to the distance cubed. Actually the period squared divided by the semi-major axis cubed is a fixed constant.

This was a major conceptual breakthrough and allowed one to describe the motions of the planets with great accuracy from a few numbers and formulae. As we will see these can be derived from Newton's laws once we move forward towards explaining motion instead of merely describing it.

Galileo Galelei (1564-1642)

Modern science techniques

1609 Galileo turns telescope to the heavens and discovers:
        1. thousands upon thousands of stars invisible to the naked eye
        2. Surface of the Sun is not perfect, has spots.
        3. There are mountains and craters on the Moon. It too is not perfect.
        4. Venus goes through phases just as the Moon does -> Copernican model explains better.
        5. Rings of Saturn
        6. Could resolve that image of planets but not stars. Also could see parallax for planets but not for stars. Stars must be very, very far away.
        7. Nebulus part of the Milky way was actually stars
        8. Four moons of Jupiter - moons clearly orbit Jupiter and not the Earth - so could other things orbit the Sun and other planets.
1610 Galileo publishes these in the Starry Messenger. Galileo became convinced that the Copernican model was actually the way the heavens moved and realized that the Physics of Aristotle stood in the way of its acceptance as much as the Catholic Church.

Galileo had other motivation and perspectives that led him to proceed to develop methods of doing science that are the foundations of modern science and these led to a new understanding of motion.

Galileo's methods

Experiments, designed to test specific hypotheses. Although careful observation dates back at least to Aristotle, Galileo was the first to refine this process with controlled experiments to test specific hypotheses.
Idealizations of real-world conditions, to eliminate, at least in one's mind, any side effects that might obscure the main effects.
Limiting the scope of the inquiry by considering only one question at a time.
Quantitative methods. Galileo went to great lengths to measure. He understood that a theory capable of making quantitative predictions was more powerful than one that could only make qualitative, descriptive predictions.

Galileo studied motion carefully.

Demonstration of Dropping Objects

One of the tenants of Aristotle's physics was that heavy things fall faster than slow things. So I will drop this sheet of paper and this large piece of chalk. The chalk weighs many times what the paper does and should get from my hand to the table much faster than the paper. I do and it does. The chalk drops directly and quickly to the table and the paper falls slowly slipping sideways and kind of floating down.

Now I crumple up the paper into a tight ball. It is the same weight as it is the same paper. I release the paper and ball simultaneously and they hit the table top essentially simultaneously. Galileo realized that air resistance was a major extraneous factor and that if one idealized an experiment without air (in vacuum) then objects would fall at the same rate.

Demonstration of balls rolling on an inclined plane

Galileo wanted to observe and measure falling but did not have sufficiently accurate instruments to measure quickly falling objects. He reasoned that if he made an inclined plane, then balls rolling down the plane would move more slowly by the ratio of the height of the inclined plane to its length and that by rolling friction would be not important. He reasoning turned out to be right and he found that the balls underwent uniform acceleration which resulted in a relation between the distance traveled and the time elapsed: the distance traveled was proportional to the square of the time elapsed. The constant of proportionality was given by the ratio of the height to the length of the inclined plane and a constant which was the acceleration of gravity 9.8 meters per second squared.

D = a t² / 2
were a is the acceleration due to gravity usually denoted by g . The factor of two comes from the fact the ball starts are rest and so at time t the ball has speed v = a t so that its average speed is v_average = v/2 = a t / 2 and the distance traveled is D = v_average t = a t² / 2 .

Demonstration of Independence of Horizontal and Vertical Motions

Demonstration of two balls released from the same height, both not initially moving in the vertical direction, both hit the bench top simultaneously. This is independent of whether one has a large horizontal velocity or not.

Issac Newton (1642-1727)