Algebra and a bit of trigonometry, both Arab embellishments (Muslim Mathematicians) of Greek and Indian achievements, represented the pinnacle of mathematical knowledge. If your own mathematical education stops short of calculus, most of what you know was taught in Moslem universities from Toledo to Timbuktu before the fourteenth century. You will also have sufficient background for this course.
In the early stages of Europe's recovery,
Thomas Aquinas and others modeled ideas taken from Greek thought,
notably the work of Aristotle,
into an all-encompassing worldview known as
It would be unfair, however, to accuse Renaissance scholars of disdain for the evidence of their own eyes. Aristotle himself had been a first-rate biologist. "One-fifth of his surviving writings are on this topic, and for thoroughness of observation and clarity of insight, they set the standard for centuries to come. He was a careful, systematic observer who believed in an order that resided in nature, waiting to be uncovered thorough observation, comparison, and classification. The great descriptive sciences, such as geology and zoology, were until recently entirely Aristotelian in their methods.
Galileo Galilei (1564-1642) Galileo's approach was a bit more sophisticated. His Aristotelian schooling had taught him to respect the value of observation. But he had even greater admiration for Aristotle's teacher Plato, who had worshipped the sublime abstract beauty of geometry. Brute nature offered nothing as perfect as the ideal triangle of dimensionless points and lines. What we scrawl on paper can be only a feeble approximation. Yet that wonders perfect triangle exists only in the human mind, visible only to pure reason. We must look beyond the imperfect world revealed by our fallible senses to uncover a higher, more perfect reality, the only fit object of study.
Galileo found a happy fusion of these contrasting approaches. Like Plato, he quested after hidden truth, written in the deep language of mathematics. But experience had shown him that reason, unaided by the senses, can be led astray. Passive observation, however, is no better for nature is too sly an adversary to reveal her most treasured secrets.
Galileo studied motion carefully.
Now I crumple up the paper into a tight ball. It is the same weight as it is the same paper. I release the paper and ball simultaneously and they hit the table top essentially simultaneously. Galileo realized that air resistance was a major extraneous factor and that if one idealized an experiment without air (in vacuum) then objects would fall at the same rate.
D = a t 2 / 2
were a is the acceleration
due to gravity usually denoted by g .
The factor of two comes from the fact the ball starts are rest
and so at time t the ball has
speed v = a t so that its average
speed is v average = v/2 = a t / 2
and the distance traveled is
D = v average t = a t 2 / 2 .
To focus his thinking, Galileo imagined the following experiment: Let a ball rool down an incline. Its speed will increase. Now give the ball a quick starting push and let it roll up an incline. It slows down, then stops and rolls back down. Suppose we make the inclies nearly horizontal.
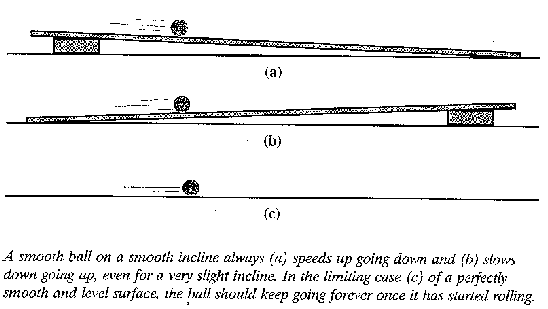
If you have ever let a ball roll down a very slight incline, you know that it is likely to slow down and come to rest, even though it is going downhill. Galieleo understood that this slowing down is due to the roughness of the incline and ball. Today we call it friction. Galileo's cfrucial stgep was to idealize the experiment by neglecting, at least in his mind, the effect of friction.
Galileo saw that neglecting friction, the ball would speed ujp on any downward incline, no matter how slight, and would speed up on any upward incline. The he took anohter characteristically brilliant step: He considered the "limiting case" of slighth inclines, namely, a peffectly horizontal surface. On a frictionless horizontal surface, the ball could neither speed up no slow down because the hnorizontal surface was intermediate between downhill and uphill. Galileo concluded that in the absences of friction, a ball that once started rolling on a horizontal surface would roll forever. This radically contradicted Aristotle's theory, which stated that continued pushing or pulling was needed to maintain violent, that is horizontal, motion.
Descartes fully embraced the rising rational spirit of his time, but he feared that something valuable wojuld be lost if the majestic world view of scholasticism was simply cast aside, with no intellectual system of comparable scope and grandeur to take its place. How were the young to be educated? It would be tragic, if the cocluded that reason was the implacable enemy of religious faith. Accordingly, he set himself the life's work of constructino a new general philosophy that would harmonize the new science with theology.
His method were far more Platonist than Galileo's. He put great stgress of the siscovery and use of first principles by pure thought, reasoning that since God is good, He would not allow a clear thinker to have a wrong idea. As a young man of the lower gentry, raised far from far from the center of French culture in Paris, he by passed a university education for training in practical matters.
Fr much of his life, Descates earned his living as a military engineer jbut hardly had a soldierly tempeament. In his day, civil engineering was the province of the military, and his work was concerned with roads and bridges as the guns and fortifications. Given a frail constitution, much of his life was spent in semiconvlescence, often living off the generosity of others.
To this day, French academic training encourages the use of his style of argument, which is Cartesian. A basic principle is isolted and followed by immpeccable deduction to conclusion of tryly astonishing and often infuriating scope. a practice that does not alwasys sit well with more empirically minded scientsts in other hands.
Descartes' contributions to mathematics went far beyond those of Galileo, but his physics is best described as flawed and incomplete. The trial of Galileo took place when Descates was in his prim, and it left a strong impression. He was loath to compromise his larger goals by getting too involved in that controversey. Most of his physics was published posthumously, in a form that reads more lkie a preliminary draft than a finished work.
Indeed, mujch of the credit for Descartes' achievements in physics should go to Christian Huygens, the som of a Dutch diplomat at whose home Descares was a frequent guest. Though he ultimately rejected Descates' philosophical system, Huygen salvaged he best parts of his physics and corrected some of the more obviousl defects.
The achievements of Descartes' mechanics fell far short of his projected goals, but he left two indelible marks on the history of physics. First he directed attention to the problem of how one objects transfers motion to another, an emphasis that helped set Newton on the right path. Second in the process of studying this problme, Descartes demonstrated the power of a remarkable format for constructin a law of nature, the conservation law.
A conservation law might be called the scientific equivalent of the Fench aphorism
A conservation law rarely provides a complete description of a process, for in spirit it implies that the details need not be considered -- they will work themselves out. Herine lies it power, for it is exempt as the outset from the necessity of dealing with a phenomenon in all its complexity. to make an anlogy with the social sciences, it is as if a political scientist worked out a means of predicting the exact electoral vote of a presidental candidate without being able to tell which way any particular state would go.
The seventeenth century was w woenderful era for the craftsmen who were fashioning better and more intricate machines, clocks being the most outstanding example. Like many scientists, Descartes came to regard, the universe as simply a machine, the work of an Almighty Inventor. The key to understanding a machine, he concluded, was to study how motion is transferred from one part ot another through direct contact. As the simplest example of this processs, he focused on colisions. Objects are in contact for a brief moment, afer which both have changed their motion.
The law that Descates used to analyze the simple problem of the collision of two bodies was that of the conservation of momentum. Momentum to Descartes was the p;roduct of the weight of a moving body and its velocity. In modern physics jargon, we substitue the word mass for weight. Weight is used to sescribe the force that gravity exerts on an object, whidh varies from place to place.. But the physicist's term mass is closely related to the common-langjuage meaning of weight. The law of momentum consedrvation asserts:
When two objects collidde, momentum may be transferred from one to the other, but the total momentum does not change.
Descartes read Galileo's work, then took it a lot further. But there was amajor difference between the two: unlike Galileo, Descartes went back to the Greeks and used a lot of their reasoning. He based his work on first principles and believed that God was benevolent and would make sure that he conducted his work correctly.
Descartes thought about Galieleo's work and wrapped it all up into something readily understandable. For example, he figure out the following which later came to be know as Newton's First Law - An object will have a constant velocity unless acted upon by an unbalanced force. Galileo had already gotten tghe first part correct about the constant velocity, but Descartes come up with the last part about forces. Descartes moved from Galileo's horizontal motion rules and inertia to include the force of gravity.
All Newton had to do for his first law was to understand Galileo's and Descartes' work and name it. Newton's brilliance really becomes apprents with his Secon Law, which tells us ho to determine the acceleration of an obect based on the forces that act on it.
An object will have a constant velocity unless acted upon by an unbalanced force.
F = m a
force on an object is equal to its mass times acceleration
For every action there is an equal and opposite
reaction.
Issac Newton (1642-1727)