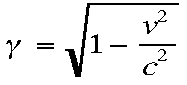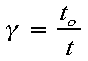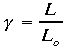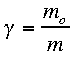Special Relativity

  1. Galilean and Newtonian Relativity
    1. Frames of Reference: The place from which an event is being observed
    2. Inertial Frame: A frame of reference that is not being accelerated
    3. Invariant Quantities: Measurements that are the same for all observers in inertial frames of reference
      1. Mass
      2. Time
      3. Distance
    4. Velocity Addition:
      1. If observers in two different frames of reference (that are in motion relative to each other) are observing motion of the same object, they will both measure it to be traveling at different speeds.
      2. Mathematically: v2 = v1 + v
        1. v: the velocity of frame one with respect to frame two
        2. v1: the velocity of the object measured by an observer in frame one.
        3. v2: the velocity of the object measured by an observer in frame two.
      3. Example:
        1. Bart is in frame one and sees Homer moving at 25 mph (v1).
        2. Nelson is in frame two and sees Bart moving at 5 mph (v).
        3. Therefore Nelson will see Homer moving at 30 mph (v2).
  2. Einstein's Relativity
    1. Origins
      1. James Clark Maxwell mathematically predicts the speed of light in a vacuum (but in what frame?)
      2. Michealson/Morely Experiment shows that the earth's motion through the solar system does not appear to affect the speed of light we observe
      3. Young Einstein contemplates what it would be like to ride with a light beam.
    2. Postulates (axioms that are to be taken for granted):
      1. The laws of physics are the same in all inertial reference frames
      2. The speed of light in a vacuum is the same for all observers (Speed of light is invariant)
    3. Consequence 1: Time Dilation
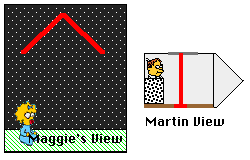
      1. The time that passes while an event is taking place is different in different frames of reference. Consider the situation depicted below. A beam oflight is fired through a small hole in the floor of a space ship. The beam travels to a mirror placed above the hole and bounces back down to the floor. This event is viewed by two observers (one in the ship and one on earth).
      2. It is clear that the two observers will see the light travel different distances. Maggie will see it traveling both vertically and horizontally, while Martin will see it traveling only vertically. If Einstein is correct and they both measure the same speed, then they must measure different times for the event to take place. Martin measures a shorter time because the light travels a shorter distance.
      3. Mathematically the two times are related by the following equations:
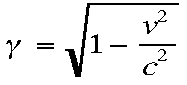
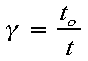
        3. to is the time that passes on the ship (Martin's time) and t is the time that passes on earth (Maggie's time)
    4. Consequence 2: Length Contraction
      1. The distance between two points in space also is different in different frames of reference. Consider the situation depicted below. An Astronaut is traveling between two planets at a very high speed. This motion is observed by the astronaut and by a person on one of the planets.
      2. Since they agree upon the relative speed of the observer with respect to the planets but disagree about the time that passes during the travel, they must also disagree about the distance that is traveled.
      3. Mathematically the two distances are related by the equation:
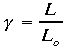
        2. Gamma is the same as it is for time and L o is the proper length (the length measured by the observer in the frame with the objects being measured)
    5. Consequence 3: Mass Increase
      1. When an object is traveling near the speed of light its mass increases if measured in other frames.
      2. Mathematically the two distances are related by the equation:
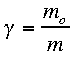
        2. Gamma is the same as it is for time and m o is the proper mass (the mass measured by the person in the frame with the object being measured)