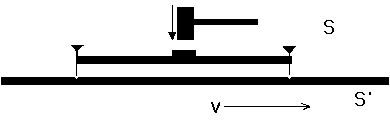
1. Point of View:
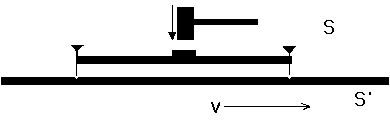
Observer O in system S places nails at the end of a meter stick
resting along his x axis, and strikes it at its midpoint
in the y direction at t = 0,
knocking it toward a rod of greater length which is moving at velocity V in the x direction.
The two nails leave two matching marks on the moving rod at the same time.
Observer O claims that Observer O',
moving with the second rod in system S',
will ascribe a greater distance L' than one meter to the separation
between the marks on his rod,
because he uses a contracted meter stick with which to measure the separation.
Further, O claims that O' will ascribe a time difference
2. Time Dilation: A rocket ship of proper length 10 m moves away from the Earth at speed 4c/5. A light signal is sent to the rocket that arrives at the rocket's tail at time zero according to the rocket clocks and Earth clocks. Calculate in both coordinate systems the time at which the light signal reaches the head of the rocket. There it is reflected back by a mirror. Calculate in both frames the time at which the light signal again reaches the tail of the rocket. Compare the elapsed times in the two frames of the round trip tail-to-head-to-tail by the light.
3. Length Paradox:
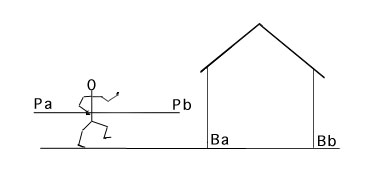In a thought experiment, a man running with speed square root(3) c /2
carries a horizontal pole having a length of 20 m in his frame.
On the ground is a barn 10 meters long in that frame and is open at both ends,
through which the runner proceeds.
Compute the length of the barn in the runner's frame S'.
Call the front and back ends of the pole Pa and Pb,
and the entry and exit ends of the barn Ba and Bb, respectively.
Find in both frames the times and positions of the following events:
(1) Pa meets Pb; (2) Pb meets Ba; (3) Pb meets Bb.
Discuss in both frames S and S' the layman's question:
"Does the pole fit in the barn?"
4. An event A occurs at (ct, x, y, z) = (0, 0, 0, 0). Another event B occurs at (3, 3, 4, 0) cm. (Light speed c = 3 x 10^{10} cm/sec.) Find a frame S' in which B precedes A in time by 1 x 10^{-10} sec. Is there a frame in which B and A occur at the same time? Suppose ctB = 6 cm instead of 3 cm. Discuss the possibilities of bringing the events into spatial and temporal coincidence.
5. If a rocket has constant acceleration in its rest frame of g = 32 ft/sec^2, how long does it take to get to a velocity of c/root(2) with respect to the Earth? Give the answer both in proper time and Earth time. Neglect the acceleration of the Earth, and gravitational fields.
6. In tests on the ground it is found that the rate of fuel consumption is proportional to the thrust, the constant of proportionality being 0.004 pound of fuel per second per pound of thrust. If the ratio of initial mass to residual mass after burnout is 10, for how long can acceleration equal to g be maintained? Consider the possible use of a multi-stage system to get to relativistic speeds.