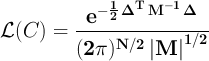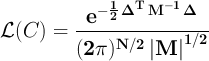CMB Data Analysis
Maximum Likelihood Analysis
Given an Np-pixel map of the sky temperature \Deltap
and a measure of the pixel-pixel correlations in the noise Npq
we want to find the most likely underlying cosmological model and parameters
that would produce the signal observed in the map. For a given model and
set of parameters we calculate the associated pixel-pixel correlations
in the CMB signal Spq. Assuming that the signal and the noise
are uncorrelated, the pixel-pixel correlations in the map - Mpq
- are simply the sum of those in the signal and the noise. Assuming that
the CMB fluctuations are Gaussian the likelihood of the particular model
and parameters is
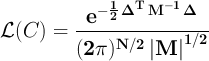Our goal is to find the best-estimated set of cosmological
parameters. That is those cosmological parameters which maximizes the likelihood
function for that class of cosmological models. A short paper outlining
the implementation of algorithms for locating the peak of the likelihood
function for a general sky temperature map can be found here
.
Timing
For a map with Np pixels, and a target cosmological
model with Nb parameters to be determined, the quadratic
estimator algorithm requires
-
(2 x Nb + 2) x Np2
x 4 bytes of disc storage.
-
2 x Np2
x 8 bytes of RAM.
-
(2 x Nb + 2/3
) x Np3
floating point operations.
assuming that
-
all the necessary matrices are simultaneously stored on disc
in single (4-byte) precision.
-
matrices are loaded into memory no more than two at a time
in double (8-byte) precision.
If the cosmological model has 10 parameters, then the computational
requirements for the current MAXIMA and BOOMERanG balloon experiments for
a single iteration of the algorithm on (i) a 600 MHz workstation and (ii)
the NERSC Cray T3E-900 (using the specified number of processors and running
at 2/3 peak) are
| Dataset |
Map Size |
Disk |
RAM |
Flops |
Serial CPU Time |
T3E Time |
| BOOMERanG N.America |
26,000 |
55 Gb |
11 Gb |
3.6 x 1014 |
7 days |
2 hours
(x 64) |
| MAXIMA-1 |
32,000 |
85 Gb |
17 Gb |
0.6 x 1015 |
12 days |
5.6 hours
(x 64) |
| MAXIMA-2 |
80,000 * |
0.5 Tb |
100 Gb |
1 x 1016 |
7 months |
9 hours
(x 512) |
| BOOMERanG Antarctica |
450,000 * |
15 Tb |
3 Tb |
2 x 1018 |
100 years |
70 days
(x 512) |
(* projected)
If we project further and consider MAP and Planck data
sets, we find even larger numbers.
Assume that the cosmological model has 20 parameters
(some cosmological & some astrophysical/experiments) parameters,
then the computational requirements for the current MAP and PLANCK missions
for a single iteration of the algorithm on (i) a 600 MHz workstation and
(ii) the NERSC Cray T3E-900 (using the specified number of processors and
running at 2/3 peak) are
| Dataset |
Map Size |
Disk |
RAM |
Flops |
Serial CPU Time |
T3E Time |
MAP
(single frequency) |
106 |
160 Tb |
16 Tb |
4 x 1019 |
2x103 years |
4 years
(x 512) |
| MAP |
105-106 |
1.6-103 Tb |
0.1-16 Tb |
4 x 1022 |
2x 101-104 years |
0.4-40 years
(x 512) |
PLANCK
(LFI) |
106-107 |
102-103 Tb |
16-1600 Tb |
4 x 1024 |
2x106 years |
200 years
(x 1024) |
PLANCK
(HFI) |
107 |
104 Tb |
1600 Tb |
4 x 1024 |
2x106 years |
200 years
(x 1024) |
(* projected)
Note that a single map containing Np
the correlation matrix is Np by Np and requires
storage size 4 Np2 in single
precision
(not exploiting symmetry or same in double precision
using the symmetry). Thus the correlation matrix for a single map with
Np = 106-107, will be 4-400 Terabytes
in size.
Return
to Planck Data Processing & Analysis page