Doppler shift
It is simplest to think of Doppler shift for sound waves. Everyone is
familiar with the sound of a passing car. When it is approaching you
the pitch is high, and it gets lower as it passes you and recedes into
the distance.
(Click here for vroom sound.)
The explanation is that the sound waves have a fixed wavelength
(distance between two crests or two troughs) only if you're not moving
relative to the source of the sound. If you are moving away from the
source (or equivalently it is receding from you) then each crest will take
a little longer to reach you, and so you'll perceive a longer wavelength.
Similarly if you're approaching the source, then you'll be meeting each crest
a little earlier, and so you'll perceive a shorter wavelength.
Since long wavelength's (low frequencies) mean lower notes and shorter
wavelengths (higher frequencies) mean higher notes, then you hear a higher
pitch if you and the source are approaching each other and a lower
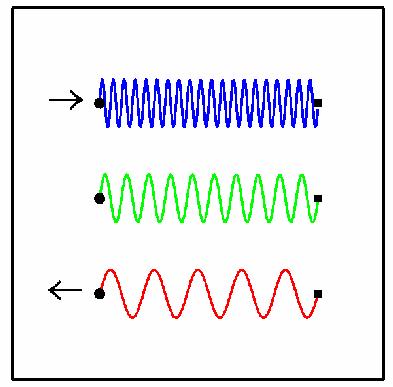
pitch if you're moving apart. This is illustrated in the
figure,
where you can think of the circle as yourself and the box as the transmitter
(or vice versa!).
The same principle applies for light as well as for sound. In detail
the amount of shift depends a little differently on the speed, since
we have to do the calculation in the context of special relativity.
But in general it's just the same: if you're approaching a light source
you see shorter wavelengths (a blue-shift), while if you're moving away
you see longer wavelengths (a red-shift).
The main difference between light and sound is that to get a detectable
Doppler effect you have to be moving at a speed which isn't tiny relative to
the speed of the waves. That's about 300 metres per second for sound,
but 300 million metres per second for light! So it's easy to hear the
change in pitch when a car whizzes past you, but it's very hard to
detect the change in color of the car! On the other hand, a very sensitive
device could measure this change, which is just what happens when a
speeding motorist is caught in a radar speed trap.
Distant galaxies are moving away from us extremely fast. So fast in fact
that it is relatively easy to measure the shift in their spectral lines.
This is evidence that the Universe is expanding, which is one of the most
important pieces of evidence in support of the Big Bang picture.
More details
Consider a distant galaxy emitting f wave crests per second.
Suppose the galaxy is moving away at speed V.
The time between wave crests is 1/f, and the galaxy moves a distance
V/f during this time. The observer measures wave crests separated not
by 1/f but by 1/f (1+V/c), including the additional time for
light to traverse the distance V/f.
So the wavelength is increased by the fractional amount V/c, and we
define this to be equal to redshift z, i.e. z=V/c, as
lambda(observed)=lambda(emitted) (1 + z).
The convention is to measure V away from the observer, so that a
velocity of approach corresponds to negative V or to a blueshift
(reduction in wavelength of emission).
Note that the redshifted frequency f is reduced, namely
f(observed) = f(emitted)/(1+z).
Recall that frequency and wavelength are reduced by f=c/lambda.
This formula for redshift is only true for velocities V that are small
compared to the speed of light. More generally, we have
z = (V/c) (1 - V^2/C^2)^{-1/2}, so that the redshift (or blueshift) of
light becomes infinite as V approaches c.
Between 1910-1920, Slipher found that many extragalactic nebulae showed
systematic redshifts. However without a convincing estimate of distance to
these nebulae, no further progress could be made.

