CMB Data Analysis
Maximum Likelihood Analysis
Given an Np-pixel map of the sky temperature \Deltap
and a measure of the pixel-pixel correlations in the noise Npq
we want to find the most likely underlying CMB signal in the map, characterised
by its power spectrum Cl . For a given power spectrum we calculate
the associated pixel-pixel correlations in the CMB signal Spq.
Assuming that the signal and the noise are uncorrelated, the pixel-pixel
correlations in the map - Mpq - are simply the sum of those
in the signal and the noise. Assuming that the CMB fluctuations are Gaussian
the likelihood of the particular power spectrum is
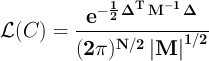Our goal is to find the power spectrum which maximizes this
likelihood function. A short paper outlining the implementation of algorithms
for locating the peak of the likelihood function for a general sky temperature
map can be found here
.
Timing
For a map with Np pixels, and a target power spectrum
sub-divided into Nb bins, the quadratic estimator algorithm
requires
-
(2 x Nb + 2) x Np2
x 4 bytes of disc storage.
-
2 x Np2
x 8 bytes of RAM.
-
(2 x Nb + 2/3
) x Np3
floating point operations.
assuming that
-
all the necessary matrices are simultaneously stored on disc
in single (4-byte) precision.
-
matrices are loaded into memory no more than two at a time
in double (8-byte) precision.
If the power spectrum is divided into 20 multipole bins,
then the computational requirements for the current MAXIMA and BOOMERanG
balloon experiments for a single iteration of the algorithm on (i) a 600
MHz workstation and (ii) the NERSC Cray T3E-900 (using the specified number
of processors and running at 2/3 peak) are
| Dataset |
Map Size |
Disk |
RAM |
Flops |
Serial CPU Time |
T3E Time |
| BOOMERanG N.America |
26,000 |
110 Gb |
11 Gb |
7.1 x 1014 |
14 days |
5 hours
(x 64) |
| MAXIMA-1 |
32,000 |
170 Gb |
17 Gb |
1.3 x 1015 |
25 days |
9 hours
(x 64) |
| MAXIMA-2 |
80,000 * |
1 Tb |
100 Gb |
2.1 x 1016 |
13 months |
18 hours
(x 512) |
| BOOMERanG Antarctica |
450,000 * |
30 Tb |
3 Tb |
3.7 x 1018 |
196 years |
140 days
(x 512) |
(* projected)
If we project further and consider MAP and Planck data
sets, we find even larger numbers.
Assume that the power spectrum is divided into 1000 multipole
bins, then the computational requirements for the current MAP and
PLANCK missions for a single iteration of the algorithm on (i) a 600 MHz
workstation and (ii) the NERSC Cray T3E-900 (using the specified number
of processors and running at 2/3 peak) are
| Dataset |
Map Size |
Disk |
RAM |
Flops |
Serial CPU Time |
T3E Time |
MAP
(single frequency) |
106 |
8 x 103 Tb |
16 Tb |
2 x 1021 |
105 years |
200 years
(x 512) |
| MAP |
105-106 |
80-105 Tb |
0.1-16 Tb |
2 x 1022 |
103-106 years |
2-2000 years
(x 512) |
PLANCK
(LFI) |
106-107 |
104-105 Tb |
16-1600 Tb |
2 x 1024 |
108 years |
104 years
(x 1024) |
PLANCK
(HFI) |
107 |
106 Tb |
1600 Tb |
2 x 1024 |
108 years |
104 years
(x 1024) |
(* projected)
Note that a single map containing Np
the correlation matrix is Np by Np and requires
storage size 4 Np2 in single
precision
(not exploiting symmetry or same in double precision
using the symmetry). Thus the correlation matrix for a single map with
Np = 106-107, will be 4-400 Terabytes
in size.
Return to Planck Data Processing & Analysis page