|
CMB Cosmology Research Program
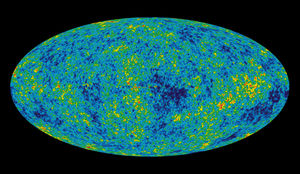
Using the cosmic microwave background (CMB) to study the creation and evolution of the universe
Text on signal flow Software concept
Neutrinos as probes of the most energetic processes in the universe
Cosmic Signal Simulations
Fast-Spherical Harmonic Transform:
We need to generate a large number of full sky realizations starting from a known spherical harmonic coefficient spectrum.
T(pixel) = Sum on L, Sum on M (-L, L) a_{LM} Y_{LM}(pixel)
We have fast code that calculates the a_{LM} for each theory and set of input parameters. The problem is to generate maps. This requires calculating the (real) spherical harmonic functions' numerical value at each pixel. We have been able to do this readily out to L = 40 for a map with 6144 pixels at a reasonable speed. Using this technique to get L = 360 and 100,000 pixels takes days to compute.
Our goal is to generate a 4 million pixel map from a power spectrum coefficients covering L =1,2000 (roughly 8 million functions to be calculated, since M goes -L,L) using a fast algorithm so that we can do this for thousands of realizations.
This can be related to the inverse of the problem - discussed below as spectral analysis - of estimating the power spectrum from the map except in spectral analysis we plan to average over M.
A paper by Muciaccia, Natoli, and Vittorio (astro-ph/9703084) develops a fast algorithm breaking the issue into two one dimensional problems: (1) a fast Fourier transform over longitude and (2) Legendre polynomial evaluation in latitude. The paper claims success with the algorithm and indicate that the next step is to implement it on parallel processors.
Another approach to fast spherical harmonic transform, similar in approach to the fast Fourier transform has been given by Healy, Rockmore, and Moore. We have copies of this paper for student use. "FFTs for the 2-Sphere - Improvements and Variations" (1996) & "An FFT for the 2-sphere and Applications", Proc of ICASSP-96 Volume 3, pp. 1323-1326.
Fast Pixelization Routines:
We have a set of pixelization routines for finding the pixel number for a given direction and direction for a given pixel number. We also have routines for finding nearest neighbors pixels. The spherical harmonics have a high degree of symmetry and this could be exploited with a suitable symmetry in the pixel scheme and the basic routine is sufficiently simple for parallelization. A pixelization scheme and making those routines fast is a potential project.
Sky Signal Simulation Framework:
This effort is to provide a simulated map of the sky for a given input frequency and instrument antenna response. It is the sum of the following seven signals extrapolated/interpolated to the given frequency and the convolved with the instrument antenna response.
Cosmic Signal
- the problem just above - the need for a fast spherical harmonic evaluation
Foregrounds 1: Clusters of Galaxies
Foregrounds 2: Extragalactic Sources
We have generated lists of extragalactic sources containing their angular position and signal flux level. The issue is to be able to convolve with antenna response function and place signal level in the map.
S = Integral of G(theta,phi) Signal
where theta and phi are the angles of the pixel from the source and G(theta,phi) is the antenna/instrument response. There are 10,000 sources to be convolved and added into 4 million pixels for each of the various antenna gain functions.
One approach past brute force is to search for only those sources near to the pixel and thus of significant signal level.
Foregrounds 3: Galactic Synchrotron Emission
We have template maps at a given frequency and resolution.
Foregrounds 4: Galactic Free-Free Emission
We have only a model of this emission.
Foregrounds 5: Galactic Dust Emission
Doug Finkbeiner has developed a high-quality, high-resolution dust map based upon two satellite missions (IRAS & COBE). This map exists at one wavelength and must be extrapolated.
Foregrounds 6: Planets and Solar System Artifacts
Similar problem to the extragalactic sources, but the planets and large asteroids of interest move noticeably. There is the issue of parallax and distance to the object of interest Thus one needs to set up an approach to handling the ephemeris for their positions.
Measured Signal Simulation Framework:
Take the sky signal and simulate the experiment, i.e. the response of the instrument during the data taking.
Instrument Noise
relatively easy Gaussian and 1/f
Scan pattern on the sky
- need to generate quickly hundreds of millions of observations - simulate scan and determine pixel number and add in instrument performance. This is relative good candidate for parallelizing. Some instruments have multiple independent elements in the focal plane and the scan several hours apart is basically independent of the previous scanning.
Data Processing of Observations
Take the (simulated or actual) signal and generate time-ordered, cleaned and calibrated data.
Large Data Set Handling
Unpack data stream, check for errors
Merge Pointing and relevant information to create complete data stream
Remove baseline and calibrate for amplitude (gain)
Data Quality Checking and Flagging
Map Generation from Observations
Take the time-ordered, clean calibrated signal and generate a sky map.
Large sparse matrix inversion or iteration procedure
Maximum entropy approach
Algorithm Development and Implementation
Separate and recover cosmological signal, foregrounds, and instrumental effects
Fast-Spherical Harmonic Transform:
Matrix Manipulation and Eigenvalue/Eigenvector Problem
Spectral Analysis
- e.g. direct spherical Fourier Transform:
one example is estimating spherical power spectrum from spherical map.
11-dimensional parameter space searching : parallelization
|

